1  Introduction: What’s the Difference?

Have you ever looked at two program descriptions and wondered how equivalent they are —or, conversely: how they can be distinguished?

I have run into this problem often, for instance when analyzing models of distributed algorithms or when devising examples for teaching. But obviously, the question already occurs every time one rewrites a program part and hopes for it to still do its job.

1  The aim was to bridge between the tools FDR2 and UPPAAL for Göthel’s dissertation (2012). The previous work I was to base the translations on had serious flaws: One approach introduced spurious deadlocks to the model, the other was unable to handle nesting of choices and parallel composition. Clearly, we had to change the encoding!

The first time I had to formally face the question was when working as a student research assistant: I was tasked with implementing a translation from the process algebra Timed CSP to Timed Automata.1 … How to tell whether the translation would properly honor the semantics of the two formalisms? Did it translate CSP terms to automata with the same meaning? Even the definition of the question is tricky, as there are different notions of what counts as “same meaning” in the semantics of programs.

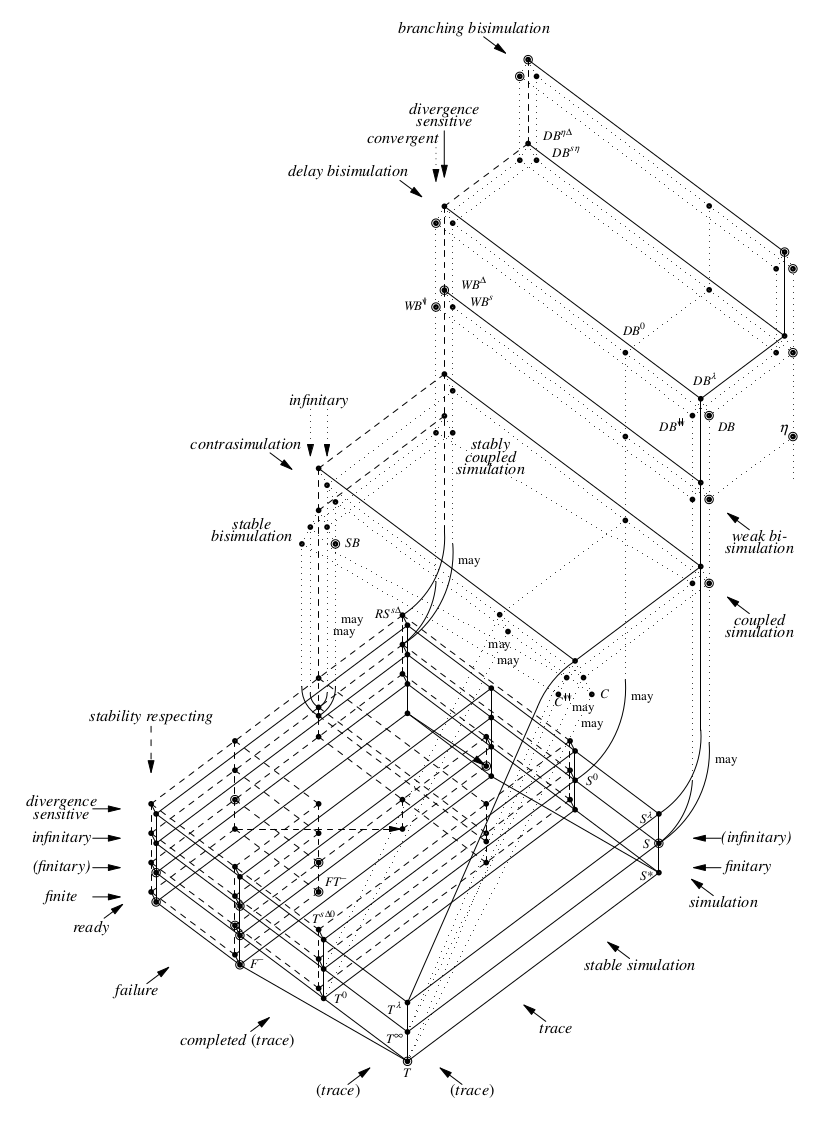
I then took my very first look into the seminal paper on the landscape of process equivalences with internal behavior, the “Linear-time–branching-time spectrum II” by van Glabbeek (1993). Its central figure, reproduced in Figure 1.1, mesmerized me. But, how to use the spectrum to decide for a given pair of processes which of the many equivalences apply, is far from straightforward. Over the years, I have learned that others too have run into this problem: For instance, Nestmann & Pierce (2000) thinking about process algebra encodings and Bell (2013) verifying compiler optimizations.

The problem can be summarized as follows:

How does one conveniently decide for a pair of systems which notions from a spectrum of behavioral equivalences equate the two?

Above question will be the research question of this thesis. We2 want to enable future researchers to tap into the wisdom of the linear-time–branching-time spectrum and to easily determine what equivalences fit their models.

2  As you might have noticed, this text uses more personal pronouns than is common in much of computer science literature. Their meaning is the same as in a lecture: “I” = “The author”; “You” = “The audience”; “We” = “The asynchronous collective of author and readers,” or sometimes “The author together with coauthors.”

1.1 Linear-Time–Branching-Time Spectroscopy

To illustrate the problem, let us look at an example that includes numerous concepts we will discuss throughout this thesis.

Example 1.1 Many verification tasks can be understood along the lines of “how equivalent” two models are. Figure 1.2 replicates a standard example, known for instance from the textbook Reactive Systems (Aceto et al., 2007): A specification of mutual exclusion \mathsf{Mx} as two alternating users \mathsf{A} and \mathsf{B} entering their critical section \mathsf{ec_A} / \mathsf{ec_B} and leaving \mathsf{lc_A} / \mathsf{lc_B} before the other may enter; and the transition system of Peterson’s (1981) mutual exclusion algorithm \mathsf{Pe}, with internal steps \color{gray}\xrightarrow{\smash{\raisebox{-2pt}{$\scriptstyle{}$}}} due to the coordination that needs to happen. (To fit on the page, \mathsf{Pe} is minimized by stability-respecting branching bisimilarity.) For \mathsf{Pe} to faithfully implement mutual exclusion, it should behave somewhat similarly to \mathsf{Mx}.

Figure 1.2: A specification of mutual exclusion \mathsf{Mx}, and Peterson’s protocol \mathsf{Pe}, minimized with respect to stability-respecting branching bisimilarity.

Semantics in concurrent models must take nondeterminism into account. Setting the degree to which nondeterminism counts induces equivalence notions with subtle differences: \mathsf{Pe} and \mathsf{Mx} weakly simulate each other, meaning that a tree of options from one process can be matched by a similar tree of the other. This implies that they have the same weak traces, that is, matching paths. However, they are not weakly bi-similar, which would require a higher degree of symmetry than mutual simulation, namely, matching absence of options. There are many more such notions, which need not be linearly ordered in how they relate processes. In our example, one might wonder: Are there notions relating the two besides mutual simulation?

For many of the existing preorders and equivalences, there are various algorithms and implementations to decide whether processes are equal. So, it would be an option to throw an array of algorithms on the transition systems of Example 1.1. But we can better!

This thesis will outline the ideas one needs to decide all equivalences in one uniform approach. In its accompanying tool equiv.io, the questions of Example 1.1 can be treated by the following query:

Example on equiv.io 
Pe = (A1 | B1 | TurnA | ReadyAf | ReadyBf)
    \ {readyAf, readyAt, setReadyAf, setReadyAt, readyBf, readyBt,
       setReadyBf, setReadyBt, turnA, turnB, setTurnA, setTurnB}
Mx = ecA.lcA.Mx + ecB.lcB.Mx

@compareSilent Pe, Mx

This query leads to the output in Figure 1.3: Weak simulation indeed is the finest equivalence to equate \mathsf{Pe} and \mathsf{Mx}! Moreover, \mathsf{Pe} is preordered to \mathsf{Mx} with respect to two more special finer notions, namely \eta-simulation and stable ready-simulation (and notions below). Intuitively, this means that \mathsf{Pe} implements \mathsf{Mx} more faithfully than pure weak simulation would demand.

How does the tool do this? The key are van Glabbeek’s “linear-time–branching-time spectrum” papers on comparative concurrency semantics (1990, 1993). They treat a zoo of distinct qualitative questions of the form “Are processes p and q equivalent with respect to notion N?”, where N would for example be trace or bisimulation equivalence. The papers unveil an underlying structure where equivalences can easily be compared with respect to their distinctive power. This is analogous to the spectrum of light where seemingly qualitative properties (“The light is blue / green / red.”) happen to be quantitative (“The distribution of wavelengths peaks at 460 / 550 / 630~\mathrm{nm}.”).

For light (i.e. electromagnetic radiation), the mix of wavelengths can be determined through a process called spectroscopy. So, we could reframe the question behind this thesis also:

Idea 1.1: Spectroscopy?

If there exists a “linear-time–branching time spectrum,” does this mean, there also is some kind of “linear-time–branching-time spectroscopy”?

This thesis answers the question positively, which is the key step to tackle our research question. One can compute what mix of (in-)distinguishabilities exists between a pair of processes, and this places the two on the spectrum of equivalences. We thus turn a set of qualitative equivalence problems into one quantitative problem of how equivalent two systems are. As we will see, this amounts to an abstract form of subtraction between programs, determining what kinds of differences an outside examiner might observe. Thereby one algorithm works for all of a spectrum.

1.2 This Thesis

Figure 1.4: The theory stack of this thesis. (TODO: Chapters, styling, links)

The algorithm at the core of this thesis describes how to decide all behavioral equivalences at once for varying spectra of equivalence using games that can count to limit possible distinctions through attacker energy budgets. More precisely, we make the following contributions, each coming with a “side quest:”

  • Chapter 2 lays some foundations and makes precise how bisimilarity games relate to grammars of distinguishing formulas of Hennessy–Milner modal logic.
    • Side quest: Certifying algorithms to check equivalences.
  • Chapter 3 shows how to understand the strong linear-time–branching-time spectrum quantitatively and formalizes the spectroscopy problem.
    • Side quest: Equivalence checking as subtraction.
  • Chapter 4 introduces the approach of characterizing equivalence spectra through a class of energy games and how to decide such games.
    • Side quest: Galois energy games.
  • Chapter 5 applies the approach to decide the whole strong spectrum through one game for linear-time–branching-time spectroscopy.
    • Side quest: Deriving efficient individual equivalence checkers.
  • WIP Chapter 6 recharts the weak spectrum of equivalences accounting for silent steps to fit our game approach.
    • Side quest: Case studies.
  • WIP Chapter 7 adapts the game for the weak spectrum of equivalences.
    • Side quest: Isabelle/HOL formalization.
  • TODO Chapter 8 showcases implementations to conveniently perform equivalence spectroscopies in web browsers.
    • Side quest: GPU parallelization.

1.3 Artifacts and Papers

This thesis ties together the work of several publications in a coherent presentation. It is written to be understandable on its own. For details, we typically refer to the original publications or to other artifacts for implementation and machine-checked proofs.

Publications. The following four publications (with me as main author) fuel the following chapters:

  • “Deciding All Behavioral Equivalences at Once: A Game for Linear-Time–Branching-Time Spectroscopy” (LMCS 2022) introduces the spectroscopy problem and the core idea to decide the whole strong spectrum using games that search trees of possible distinguishing formulas. (Conference version: TACAS 2021)
  • “Process Equivalence Problems as Energy Games” (CAV 2023a) makes a big technical leap by using energy games, removing the necessity for explicit formula construction. (Tech report: arXiv 2023b)
  • “Characterizing Contrasimilarity through Games, Modal Logic, and Complexity” (Information & Computation 2024) closes gaps in the weak spectrum of equivalences for games and their complexity and their link to modal logics. (Isabelle/HOL theory: AFP 2023; Workshop version: EXPRESS/SOS 2021)
  • “One Energy Game for the Spectrum Between Branching Bisimilarity and Weak Trace Semantics” (EXPRESS/SOS 2024) adapts the spectroscopy approach for the weak spectrum. (Tech report: Preprint 2025)

Prototype. The algorithms of this thesis have been validated through a Scala prototype implementation. Throughout the thesis, many examples come with listings of equiv.io input and a link to try it out the browser. You have already seen one such example for Peterson’s mutex in Section 1.1. The source is available openly at https://github.com/benkeks/equivalence-fiddle.

Isabelle formalization. Instead of swamping the document with technical proofs, these are contained in machine-checkable Isabelle/HOL theories.

Student theses. Some parts of this thesis strongly rely on student work that I have supervised, in particular, on the following theses:

  • Trzeciakiewicz (2021): Linear-Time–Branching-Time Spectroscopy as an Educational Web Browser Game provides a computer game version of the spectroscopy procedure to be discussed in Section 8.3.1.
  • Ozegowski (2023): Integration eines generischen Äquivalenzprüfers in CAAL extends the Concurrency Workbench Aalborg Edition with a spectroscopy feature, reported in Section 8.3.2.
  • Mattes (2024): Measuring Expressive Power of HML Formulas in Isabelle/HOL proves the approach to modal characterization of Section 3.2.
  • Vogel (2024): Accelerating Process Equivalence Energy Games using WebGPU, topic of Section 8.2, allows massive parallelization on the GPU of key parts of our algorithm.
  • Lemke (2024): A Formal Proof of Decidability of Multi-Weighted Declining Energy Games formalizes the fixedpoint algorithm of Section 4.3.

Other publications. Only indirectly connected to this dissertation project are my prior publications in leading me to topic and techniques:

  • Bisping et al. (2016, ITP): “Mechanical Verification of a Constructive Proof for FLP.”
  • Bisping & Nestmann (2019, TACAS): “Computing Coupled Similarity.”
  • Bisping et al. (2020, Acta Informatica): “Coupled similarity: the first 32 years.”

Other Bachelor theses. During my dissertation project, I also supervised several other Bachelor theses, many of which played important roles in shaping the research. Although they do not appear directly on the following pages, I want to acknowledge the students’ vital contributions to the research.

  • Peacock (2020): Process Equivalences as a Video Game
  • Lê (2020): Implementing Coupled Similarity as an Automated Checker for mCRL2
  • Wrusch (2020): Ein Computerspiel zum Erlernen von Verhaltensäquivalenzen
  • Reichert (2020): Visualising and Model Checking Counterfactuals
  • Wittig (2020): Charting the Jungle of Process Calculi Encodings
  • Bulik (2021): Statically Analysing Inter-Process Communication in Elixir Programs
  • Montanari (2021): Kontrasimulation als Spiel
  • Pohlmann (2021): Reducing Strong Reactive Bisimilarity to Strong Bisimilarity
  • England (2021): HML Synthesis of Distinguished Processes
  • Duong (2022): Developing an Educational Tool for Linear-Time–Branching-Time Spectroscopy
  • Alshukairi (2022): Automatisierte Reduktion von reaktiver zu starker Bisimilarität
  • Adler (2022): Simulation fehlertoleranter Konsensalgorithmen in Hash.ai
  • Sandt (2022): A Video Game about Reactive Bisimilarity
  • Lönne (2023): An Educational Computer Game about Counterfactual Truth Conditions
  • Hauschild (2023): Nonlinear Counterfactuals in Isabelle/HOL
  • Stöcker (2024): Higher-Order Diadic µ-Calculus—An Efficient Framework for Checking Process Equivalences?
  • Kurzan (2024): Implementierung eines Contrasimilarity-Checkers für mCRL2

This thesis itself. This document itself is created using Quarto (2025). Its HTML version is deployed to https://benkeks.github.io/generalized-equivalence-checking/. One can find its source at https://github.com/benkeks/generalized-equivalence-checking/.